Update to the below:
There are some images and colour combinations that did show odd results. Check out my post further down this thread.
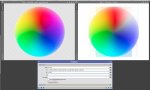
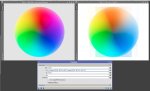
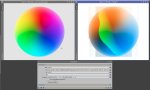
Now I'm using the following formulae, just boosting G to the min of R and B. See the link above for effects on a colour wheel showing how it much better targets just the magenta.
R: $T[0]
G: iif(min($T[0],$T[2])>$T[1],min($T[0],$T[2]),$T[1])
B: $T[2]
The attached zip file has been updated to use this formula.
---------------------------------------------
Original post:
Not sure if this has been done before, but I had this idea recently on how to get rid of the magenta stars in SHO narrowband images due to the red SII and blue OIII channels needing to be stretched so much to balance strong G Ha. A common Photoshop method I've seen is to do a selection based on colour (magenta), and desaturate it.
It occurred to me that with PixelMath we may be able to achieve something like this. We could detect if a pixel is magenta by checking if it's R and B channels were of similar value (within some acceptable range), and if they both were significantly brighter than the G channel.
With this in mind, I came up with the following formulae. I found some stars needed a luminance rule in there too.
R: $T[0]
G: iif((CIEL($T)>MIN_BRIGHTNESS)||((min($T[0],$T[2])/(max($T[0],$T[2])>MAGENTA_DEFN))&&(mean($T[0],$T[2])>$T[1])),mean($T[0],$T[2]),$T[1])
B: $T[2]
Symbols: MAGENTA_DEFN = 0.9, MIN_BRIGHTNESS = 0.9
Attached are some sample before and after images (not my images, but have sought the approval of the image owners where possible. Some were from a Google image search). Seems to work ok to me. Thoughts? Any improvements or suggestions on the above?
I'm just hoping it is a quick and simple solution to what seems to be a common issue with narrowband images. Just drag and drop the attached process icon on your final narrowband image with magenta stars and they're gone.
There are some images and colour combinations that did show odd results. Check out my post further down this thread.
Now I'm using the following formulae, just boosting G to the min of R and B. See the link above for effects on a colour wheel showing how it much better targets just the magenta.
R: $T[0]
G: iif(min($T[0],$T[2])>$T[1],min($T[0],$T[2]),$T[1])
B: $T[2]
The attached zip file has been updated to use this formula.
---------------------------------------------
Original post:
Not sure if this has been done before, but I had this idea recently on how to get rid of the magenta stars in SHO narrowband images due to the red SII and blue OIII channels needing to be stretched so much to balance strong G Ha. A common Photoshop method I've seen is to do a selection based on colour (magenta), and desaturate it.
It occurred to me that with PixelMath we may be able to achieve something like this. We could detect if a pixel is magenta by checking if it's R and B channels were of similar value (within some acceptable range), and if they both were significantly brighter than the G channel.
With this in mind, I came up with the following formulae. I found some stars needed a luminance rule in there too.
R: $T[0]
G: iif((CIEL($T)>MIN_BRIGHTNESS)||((min($T[0],$T[2])/(max($T[0],$T[2])>MAGENTA_DEFN))&&(mean($T[0],$T[2])>$T[1])),mean($T[0],$T[2]),$T[1])
B: $T[2]
Symbols: MAGENTA_DEFN = 0.9, MIN_BRIGHTNESS = 0.9
Attached are some sample before and after images (not my images, but have sought the approval of the image owners where possible. Some were from a Google image search). Seems to work ok to me. Thoughts? Any improvements or suggestions on the above?
I'm just hoping it is a quick and simple solution to what seems to be a common issue with narrowband images. Just drag and drop the attached process icon on your final narrowband image with magenta stars and they're gone.