24-Bit Screen LUTs in PixInsight 1.8

Tutorial by Juan Conejero (PTeam)

This document is an adaptation of a tutorial posted by the author on PixInsight Forum in November of 2013.
Original forum thread.

---

Lookup Tables

One of the most important new features introduced in the new version 1.8.0 of PixInsight is 24-bit screen transfer function lookup tables. Before I put several examples to show how 24-bit STFs work in practice, let me explain briefly what this stuff is all about.

A lookup table (LUT) is a list of precomputed function values at specific points of interest. For example, suppose that you need to evaluate the same function y = f(x) repeated times to perform a given task, but you know in advance that an 80% of function evaluations (for example) will be done, on average, for a reduced set of 1000 particular values of the independent variable x. If you precompute those 1000 function values and store them in a fast-access table, such as a random-access array in memory, then you can transform your function as follows:

   if x belongs to the set of 1000 precomputed values, then
      look for the corresponding table element, which is the value of f(x).
   else
      compute f(x).

Transformed this way, your task can be executed much faster because you replace an 80% of function evaluations with fast table lookups, which can be done in constant time. In fact, if your f(x) is relatively expensive, your task will run approximately an 80% faster thanks to this trick. This scheme is a special form of hash table, and is the basic concept behind LUTs.

In its simplest and most efficient form, a LUT is used to discretize a function for a finite set of integer values of x. This is just what PixInsight does to represent some types of images on the screen. Since the screen (as seen by a software application) is an 8-bit device, each screen pixel can only take 2⁸ = 256 different values for each color, from 0 (black) to 255 (white). For RGB color images, this makes up a set of 2^3*8 = 16,777,216 representable colors. For example, to represent a 16-bit integer image on the screen, we have a precomputed LUT of 65,536 (= 2¹⁶) 8-bit values, where each LUT entry is equal to its table position divided by 257 (=65535/255) and rounded to the nearest integer:

   round(0/257)=0, round(1/257)=0, round(2/257)=0, ..., round(65535/257)=255.

This allows us to render a 16-bit image much faster because we can replace a floating-point multiplication (followed by a rounding operation) by a simple table lookup operation. For other pixel sample formats a LUT is impractical in this context; for example, for 32-bit integer images the same scheme would require a LUT of length 2³², which would occupy 4 gigabytes.

Screen Transfer Functions

A screen transfer function (STF) is just a histogram transformation that PixInsight applies to each pixel of an image to represent it on the screen. This allows us to see how a linear image would look like after a nonlinear intensity transformation, but without changing the actual pixel values. STFs are an essential component of PixInsight's graphical interface because they make it possible to work directly with linear images, which has important advantages in many cases (background modelling, noise reduction, multiscale processing) and is absolutely necessary in others (color calibration, deconvolution). The most computationally expensive part of the STF is a midtones transfer function (MTF):

where m is the midtones balance parameter: the lower the midtones balance value, the more aggressive nonlinear stretch is applied by the function. The MTF isn't too complicated: if properly implemented, it requires two multiplications, one division, one sum and two subtractions for each pixel, all of them floating point operations. This may seem quite cheap, but if we have to repeat it several millions of times to perform a real-time task such as rendering an image on the screen, then we have a serious problem. As you probably have figured out at this point, to perform this task in real time we use a precomputed LUT to discretize the STF of each image.

In previous versions of PixInsight, STF LUTs were always generated with 16-bit precision, that is, each STF LUT had only 65,536 elements. While this is more than sufficient for most well-exposed linear images, it is clearly insufficient in some important cases. When the number of precomputed LUT elements is not sufficient to represent the STF accurately, the resulting screen rendition shows posterization.

Posterization

Posterization leads to complete loss of image detail on certain areas of an image's screen representation as a result of excessive simplification. This happens frequently with high dynamic range (HDR) images, which usually require extremely aggressive midtones transfer functions.

The following screenshot shows an HDR image of the M42 region by Vicent Peris and José Luis Lamadrid:

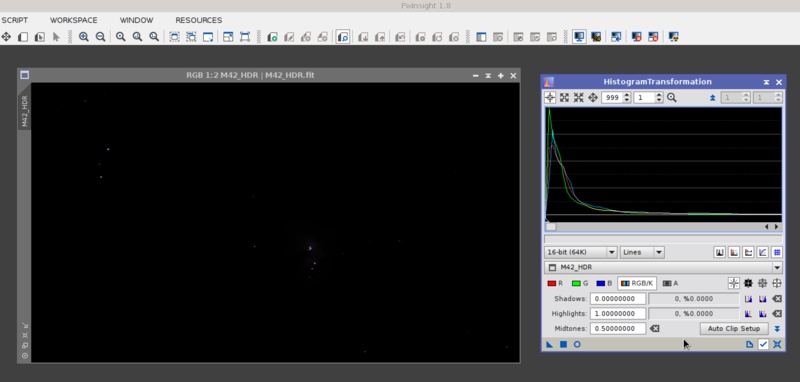
On the screenshot above we have a good example of how linear images usually look like: black. Of course, the histogram explains why: most of the data are concentrated in a narrow peak close to the beginning of the numeric range. As a result of this distribution of the data, we simply cannot see the image. In the case of linear HDR images, the problem becomes severe: the histogram peak is much narrower, and it is even much closer to zero. On the screenshot, note that the histogram is being represented with 999x magnification on the horizontal axis—the maximum zoom factor available on the HistogramTransformation tool, in fact.

What happens if we apply a 16-bit STF to this image? Since the required midtones transfer curve is very steep, it requires much more than what 16-bit integers can offer to represent its initial—almost vertical—slope. The result is severe posterization:

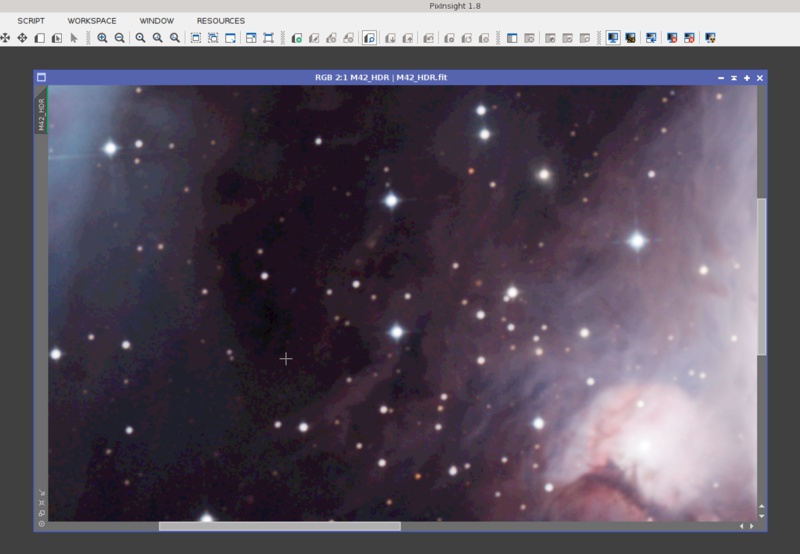
Posterization is much worse than ugly screen representations: it simply makes it very difficult—and in some cases completely impossible—to work with these images in the linear stage. This is obviously not what you need and want.

Since version 1.8.0, PixInsight can generate and use 24-bit LUTs to discretize STFs. With 24 bits we have 16,777,216 discretization points, or 256 times more resolution than 16-bit LUTs. Of course, this also means 256 times more computational work to generate each LUT, and 256 times more memory space requirements (16 megabytes for each color channel instead of 64 kilobytes). This explains why 16-bit LUTs are still used by default, since they are sufficient for most linear images.

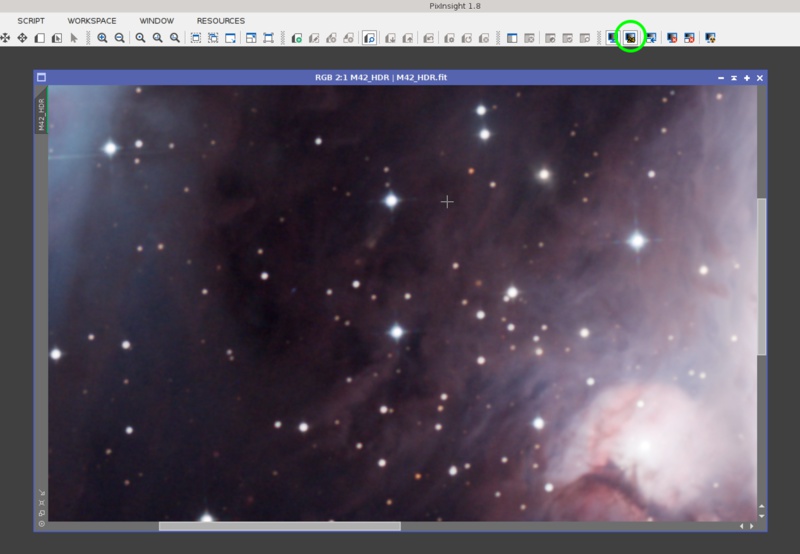
With a 24-bit STF, the same M42 HDR image shows no posterization at all:

More Posterization!

Do you think that the above M42 image is a good example of posterization? I was thinking the same, and was proud of the new 20-bit STFs that were working so nicely, when Vicent Peris uploaded the following:

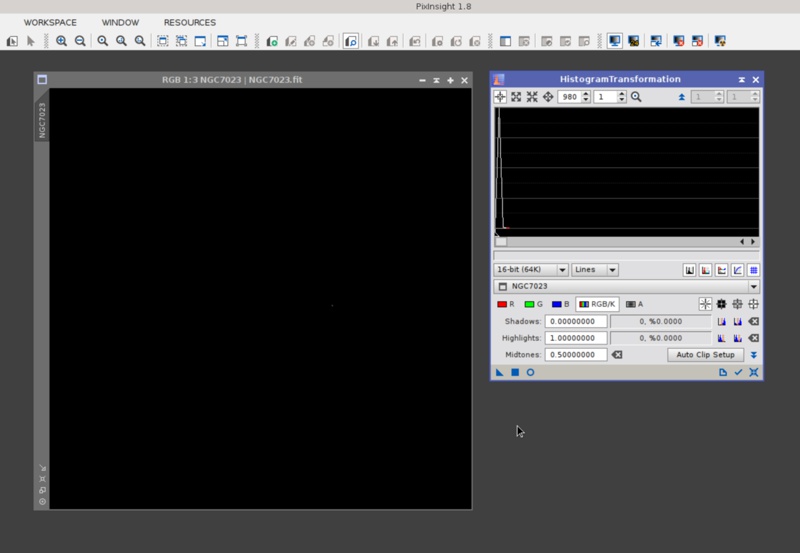
Look at the histogram to understand why this image changed our development plans. With a 16-bit STF—and exactly the same with a 20-bit STF—, this image simply redefines the concept of posterization:

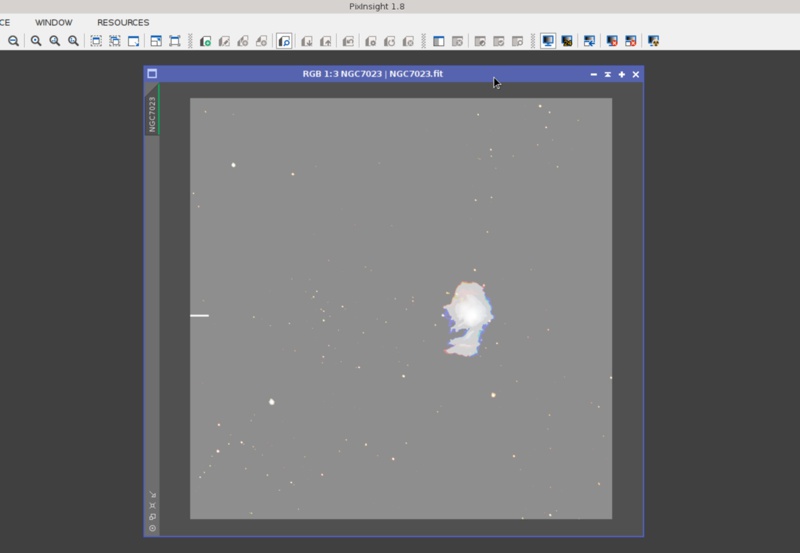
Fortunately, a 24-bit STF provides a much better screen rendition:

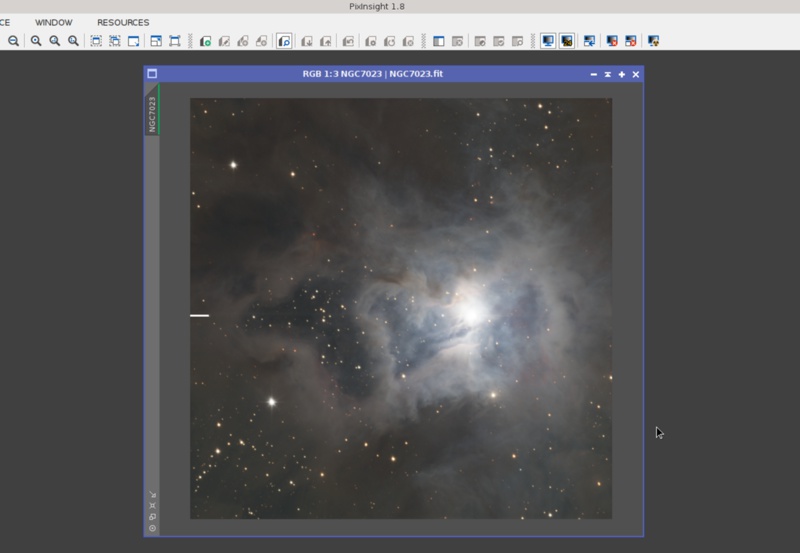
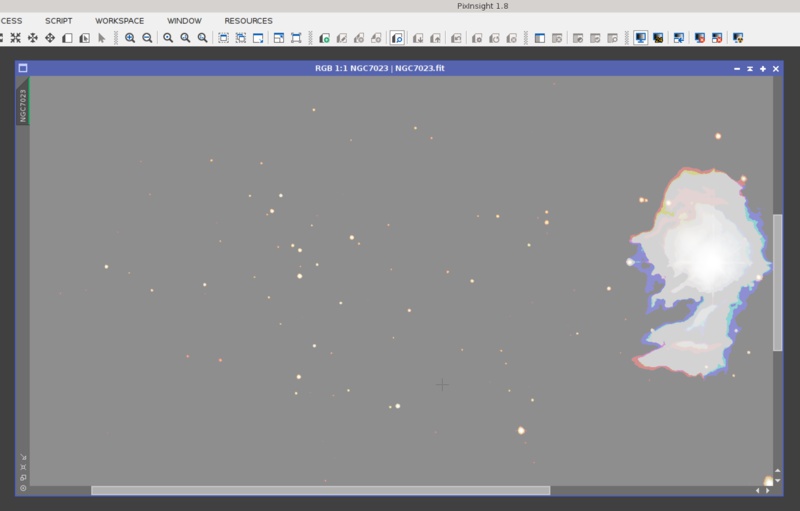
With a 24-bit STF this image still shows a bit of posterization on its darkest areas, but nothing problematic. To be completely free from posterization, this image would require a 29-bit LUT, which is impractical for obvious reasons (it would occupy 1.5 GB for a color image). Here are enlarged views for better comparison:

With 16-bit and 20-bit STF:

With 24-bit STF:

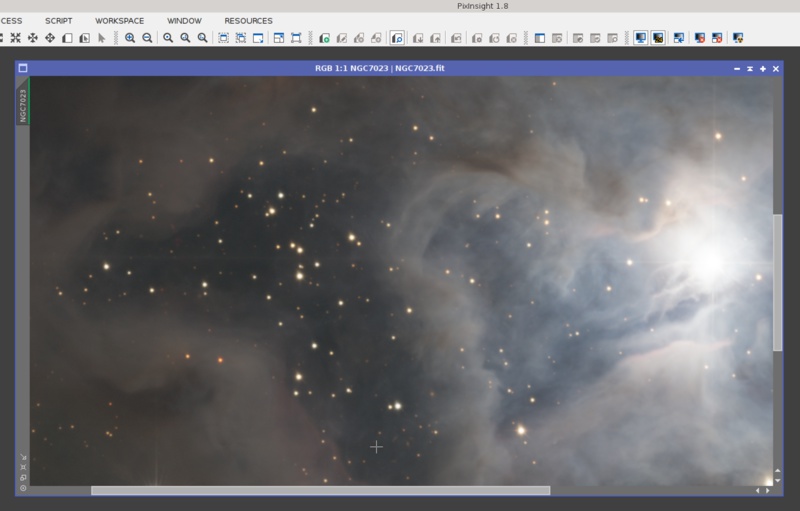
Finally, I want to point out the fact that 24-bit STFs are not only useful for HDR images. They provide much more accurate renditions of weak raw images, where the histogram peaks are comparatively narrow and close to zero, and also for images with extremely smooth gradients, such as background models.