SubframeSelector Weighting Tool (SWT), v 1.0.0
Alex Woronow & Jim Hunt
This document describes a user-friendly spreadsheet designed to assist in the comprehensive, methodical assignment of relative weights to subframes. The tool, named the “SubframeSelector Weighting Tool” (SWT), interacts with PixInsight’s SubframeSelector script, serving both as the source of its inputs and as the recipient of its weighting-equation output. We explain the rationale for the approach implemented within SWT and the procedural steps required to generate its weighting-equation output. The current version of SWT can be downloaded here
https://tinyurl.com/SWTandDoc100
Statement of problem
Single-Image S/N
Relevant Quality Variable
Something about SWT’s internal workings
Scaling within Variables
Scaling among Variables
Flow of Actions
The SWT’s User Interface
Contemplating and Evaluating the Relations among Input Parameters
Statement of Problem
By default, relative weights of each image in PixInsight apparently rest upon the calculation of each image’s signal-to-noise ratio (S/N). The efficacy of this approach has received some skepticism and subsequent suggestions that star eccentricity, FWHM, and perhaps other parameters should figure into the subframe weightings. The SWT Excel spreadsheets provide a conduit for the weighted inclusion of these additional variables. Anywhere from 1 to 4 of the variables produced by SubframeSelector can be used and weighted in any manner deemed effective. (see attachment)
Other spreadsheet-based tools able to generate a subframe weighting-equation exist, and they provided the inspiration for this approach, particularly the instrumental work of David Ault (see here). I hope this implementation proves useful too. At a meeting of imagers, one speaker suggested tossing in all your subframes and let the stacking sort them out. Stacking does not sort them out, at least not optimally. Simply, if in your data set of 20 subframes there is some subframe, B, that has over-sized stars, but frames Y and Z even have larger ones, then stacking may toss Y and Z, but leave B in, thus degrading your stack. SWT is designed to catch the fact that B is abnormal too and reject it, at your discretion.
The following section describes the problem with using the S/N as the sole variable for assigning subframe weights as well as allusions to the problem of even defining S/N for a single frame. The rest of this section is optional and can be skipped if you know what you want for weighting variables and just want to know how to use the spreadsheet. But, we advise using SWT after the subs have been calibrated.
Single-Image S/N
For the moment, ignore the fact that image S/N has more than one way it can be calculated (with different results for each). A deeper problem apparently exists, i.e., for a single-image S/N cannot reliably be quantified at all. One internet author puts it like this: ask someone to tell you an arbitrary number. For discussion, imagine they say, “5.” Then ask them, “What is the uncertainty in 5?” No rational response exists to your question, of course. Likewise no agreed-upon response exists to the question, “What is the S/N value for a single image?” Nonetheless, many programs, including PixInsight (see here), attempt to numerically circumvent the problem, probably with varying degrees of success. As of this writing (May, 2020), Juan Conejero posed a comment on the PI forum to the effect that the current noise evaluation is going to be replaced by a better one in an upcoming release. Noise evaluation is far from cut-and-dried.
Now, whatever your personal take-away from the above might be, we move on to discuss alternative variables for assessing subframe qualities or weights. Other clearly measurable variables do exist in an image, and speak to elements of the relative quality of an image compared to the ensemble of subframes. Thus they may well be more adjusted to the particular type of target you have.
Relevant Quality Variables
Other image parameters, besides the frail S/N ratio, speak to a subframe’s worth in a stack of similar subframes. Often those variables receive scrutiny during frame-by-frame blink comparison. For instance, visually assessing star ellipticity, FWHM, and other measures (e.g., using blinking) could help an image processor to eliminate wildly deviant frames. But one might argue that a frame with some modest degree of star ellipticity, for instance, might suffer a justifiably lower weight without being completely eliminated.
Besides the obviously inferior frames, we might wonder if some variable used to quantify image quality might sometimes be misleading. For instance, does FWHM or ellipticity decrease as a light haze or sky glow impinges on the imaged scene? I’m not sure about the answer, but it worries me that it might. Sometimes the number of stars in an image strongly, negatively correlates with FWHM and even ellipticity! Maybe those variables should not have a large say in a final frame’s weight? I tend to favor StarSupport as an important subframe-weight parameter. If the sky becomes hazy or light pollution rises, StarSupport decreases, as it would if the focus drifted, turbulence increased or tracking-accuracy declined. All these either spread the star light more broadly so that fainter stars fail to be recognized or mask the fainter stars with an increase in the background. However, Mike Schuster (here) notes that under-sampled images (wide field, low resolution images), may not separate stars and noise well. Also, subs with abundant shot noise may give false, elevated star counts. This can be somewhat ameliorated during calibration and using CosmeticCorrection.
SWT also includes two variables that encode the behavior of the median value of a subframe: MedianHi” and “MedianLow”. The former could be used if you believe that higher values of the median indicate better subframes, as might be the case if a nebula pervades the image. The former could be used if you believe that smaller values of the median indicate better images, such as an image of a small galaxy in a field of stars and darkness. Be watchful of these measures, however. You could have a very dark background because you forgot to remove the cover from the camera lens (or…).
Something about SWT’s internal workings
The Less Arbitrary Part—Scaling Within a Variable
Consider a single quality-evaluation variable measured across a number of subframes. That variable will have a range of values from least favorable (XA) to most favorable (XZ). A measured intermediate value of Xi for some subframe image in this set might reasonably be assigned a weight (wi) proportional to its position in the range of values; e.g.,
Such a linear relationship could be specified for each variable, i, producing a set of variable-by-variable weights for each subframe. This is the approach used in my SWT with the addition of a “pedestal.”
The More Arbitrary Part—Scaling Among Variables
Combining individual variable weights from Eqn 1 into an ensemble weight involves “user’s prerogatives.” That is, based on your individual experiences and perspectives, and considering the particular attributes of the image-set at hand, the ensemble of within-variable weights can be combined by relative weighting factors (denoted by F). For example, say you measured the variables V1, V2, V3 on some image j. Those variables would, by Eqn 1, have corresponding weights w1,w2,w3 for that one image. Consistent with our individual knowledge and preferences, we would assign weighting factors F1 F2 F3 to each w such that F1 + F2 + F3 = 1. We can then obtain an overall weight, Wj, for our single subframe frame. For example, the kth frame’s weight would be
In SWT, the final values of the frame weights also can be rescaled between a pedestal value (minimum frame weight) and 1.0, and nonlinearly gamma-stretched to span that interval, at the discretion of the user.
The Flow of Action
Load images for weighting into SubframeSelector script of PixInsight. Usually the images analyzed in a single pass would be a homogeneous set (for instance, all light frames of a single subject shot through a single filter). Additionally, these should be raw, calibrated and cosmetically corrected frames and not stretched.
Use SubframeSelector’s “Measure” feature to produce a table of values of variables for each frame.
Output the table in a csv format using SubframeSelector’s “Save CSV” button.
Open the SWT workbook and Enable Content, if necessary (top yellow banner).
Select the four variables you want to start, you can select others any time.
Click the Read CSV File button in the Excel spreadsheet. Select and load the desired file.
Adjust weights, Pedestal, Stretch, etc. until you have a satisfactory relationship for accepting and rejecting subframes.
If you change variables in table I, the spreadsheet will re-read the data to implement the new selection.
Click Copy SS Equation button to copy the equation generated by the Subframe Weighting Tool to the clipboard. Then paste the equation into Expressions>Weighting field of the SubframeSelector. Click the arrow at the right of the Expression Weighting field to implement the equation you just pasted.
Set SubframeSelector’s Approval level to the desired value—usually the one you settled upon in SWT. Click the arrow to the right of the field where you pasted the level to implement the new criterion. (Note, your equation in this field should look something like this: “Weight>=0.4”.)
CHECK THAT THE WEIGHTS CALCULATED IN SUBFRAMESELECTOR MATCH THOSE IN SWT. If they do not, either the wrong information was pasted into SubframeSelector or you did not click the arrows to update SubframeSelector to the information you pasted in.
Set SubframeSelector’s name for the new weights it will generate and the output path and click “Output Subframes”. The name SSWEIGHT seems appropriate.
The images output in the previous step may be used in PixInsight’s ImageIntegration procedure, specifying the name you specified for the new weighting variable (e.g., SSWEIGHT). The integrated image now will reflect the user-defined weights.
If you need duplicate sheets for different filters, use the Copy Sheet button.
Another used for the weights generated by SWT is to select a subframe for the reference alignment frame. The subframe with a large number of stars and a small number value for the FWHM would present a logical choice. If the compulsion drives you, you could combine all the fames from every filter on one spreadsheet and select a winner. Alternatively, look for the best Luminosity frame or the best green-filter frame.
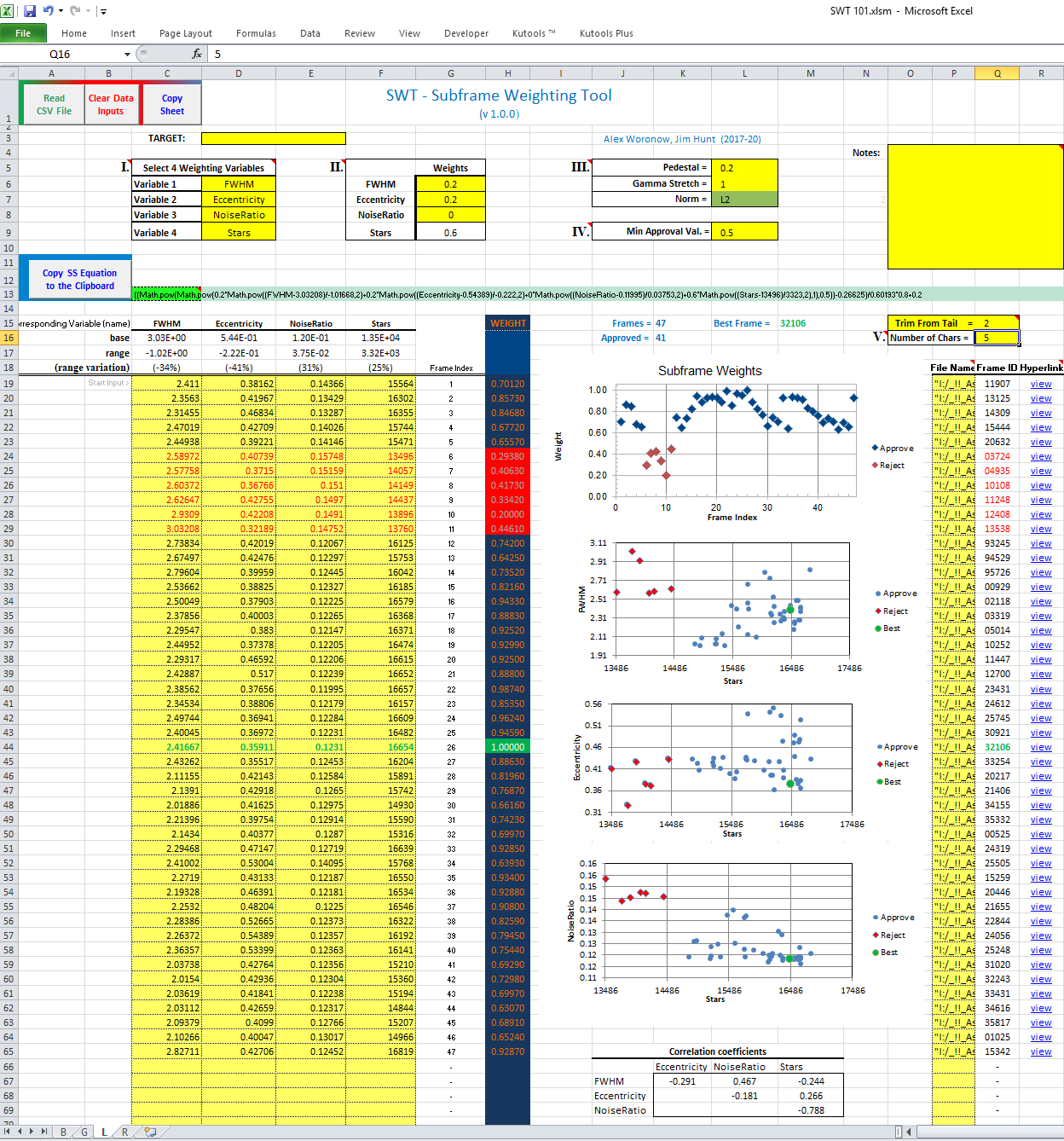
The SWT’s User Interface
Input fields have yellow backgrounds. A detected input error turns the offending cell’s background to red. Computed-values cells in the spreadsheet that have a white background or a deep-blue background (e.g., the “WEIGHT” column), should not be edited. Many of them contain equations; others have text designed for special purposes. The bright green cell is the one that is copied to the clipboard for pasting into the weighting equation in the SubframeSelector script. The less bright green cells simply provide a background highlighting the equation.
The discussion now references the spreadsheet entry fields I through V as labeled on the spreadsheets.
Select 4 variables to participate in the weighting from the drop-down lists. You may assign a zero weight to a variable. The fourth variable, at the bottom of the list, is the variable that will be used as the independent variable in the variable-variable cross plots.
The weights [0.0, 1.0] to assign to each of the first three variables. The weight of the final variable is calculated such that the sum of the weights equals 1.0.
Controls for the pedestal and stretch of the distribution of the subframe weights.
Pedestal: controls the minimum subframe weight that will be assigned. At least one subframe will have that weight and at least one weight will be 1.0.
Gamma Stretch: a stretching exponent (> 0) that affects the distribution of the weights within the interval [Pedestal, 1.0].
Norm: This has two values selected from a drop-down menu. An L1-measure weights the variables by their distance from the worst value for each weighting variable. An L2-measure uses the square of that distance. (Use L2 if in doubt. Usually the two give pretty much the same weights.)
Min. Approval Value: If a subframe’s weight is less than this value, that subframe has red markers on the plots and in the tables. Expectedly, SubframeSelector (if fed proper inputs from SWT) will not retain red-marker subframes in its output.
Locate the part of the sub-frame name to display: E.g., say the location of the last character in the ID lies back N characters from the “.” of the file extension. You would enter N-1 in this field to see the ID. The “Trim From…” has a dropdown menu to facilitate trimming from the beginning or end of the frame ID.
The function of the other (yellow) user-input fields should be rather obvious.
Contemplating and Evaluating the Relations among Input Parameters
Before running Subframe selector, blink your images! Images that appear “unlike the others” are also not statically members of the group and will distort the weights. Remove them before using SWT!!! Remove any that have strongly elliptical stars, star trails, high noise, low signal, etc.
To adjust the relative variable Weightings and the Stretch, Pedestal, and Approval level, garner some insights from three sources:
1. The top graph: Does the overall spread of weights look reasonable and functional? For instance, if all the frames are expected (from blinking, say) to have pretty similar qualities, maybe a higher-value pedestal, to compress all the weights to a small range, may be appropriate.
2. The other three graphs: Are the rejected subframes (red) and the best subframe (green) credible given what you know about the image acquisition? Cross-check rejected subframes among graphs and the tabulated data—does rejection/Approval make sense?
3. If need be, examine the frames that have unexpected weights. (Click the “Hyperlink>View” to open the frame in your default viewer, probably PI.)
4. Most importantly, scroll down to examine the correlation table below the graphs: Are some variables strongly correlated? If so, then perhaps you want to down-weight one of the two correlated variables as the other variable partially accounts for its variations already. Also, do the correlations suggest some prevailing effect, such as more stars correlate positively with greater eccentricity…what is that trying to tell you?
5. The “range variability” of each variable (the row above the pasted data): Variables with noticeably smaller ranges than the other variables may indicate that the variations are unimportant (i.e., largely random variations or measurement uncertainties). In that case, down-weighting the narrowly varying variables could be justified. You might look for another variable to use instead: one that varies more widely yet quantifies frame quality as well.
We hope you find this spreadsheet useful. You may contact us through alex@awkml.com . Please report any bugs and suggestions for improvements and additions. Also, in published images, e.g., on Astrobin or Flicker, Simply reference “SWT”- Thanks!
Alex Woronow & Jim Hunt
This document describes a user-friendly spreadsheet designed to assist in the comprehensive, methodical assignment of relative weights to subframes. The tool, named the “SubframeSelector Weighting Tool” (SWT), interacts with PixInsight’s SubframeSelector script, serving both as the source of its inputs and as the recipient of its weighting-equation output. We explain the rationale for the approach implemented within SWT and the procedural steps required to generate its weighting-equation output. The current version of SWT can be downloaded here
https://tinyurl.com/SWTandDoc100
Statement of problem
Single-Image S/N
Relevant Quality Variable
Something about SWT’s internal workings
Scaling within Variables
Scaling among Variables
Flow of Actions
The SWT’s User Interface
Contemplating and Evaluating the Relations among Input Parameters
Statement of Problem
By default, relative weights of each image in PixInsight apparently rest upon the calculation of each image’s signal-to-noise ratio (S/N). The efficacy of this approach has received some skepticism and subsequent suggestions that star eccentricity, FWHM, and perhaps other parameters should figure into the subframe weightings. The SWT Excel spreadsheets provide a conduit for the weighted inclusion of these additional variables. Anywhere from 1 to 4 of the variables produced by SubframeSelector can be used and weighted in any manner deemed effective. (see attachment)
Other spreadsheet-based tools able to generate a subframe weighting-equation exist, and they provided the inspiration for this approach, particularly the instrumental work of David Ault (see here). I hope this implementation proves useful too. At a meeting of imagers, one speaker suggested tossing in all your subframes and let the stacking sort them out. Stacking does not sort them out, at least not optimally. Simply, if in your data set of 20 subframes there is some subframe, B, that has over-sized stars, but frames Y and Z even have larger ones, then stacking may toss Y and Z, but leave B in, thus degrading your stack. SWT is designed to catch the fact that B is abnormal too and reject it, at your discretion.
The following section describes the problem with using the S/N as the sole variable for assigning subframe weights as well as allusions to the problem of even defining S/N for a single frame. The rest of this section is optional and can be skipped if you know what you want for weighting variables and just want to know how to use the spreadsheet. But, we advise using SWT after the subs have been calibrated.
Single-Image S/N
For the moment, ignore the fact that image S/N has more than one way it can be calculated (with different results for each). A deeper problem apparently exists, i.e., for a single-image S/N cannot reliably be quantified at all. One internet author puts it like this: ask someone to tell you an arbitrary number. For discussion, imagine they say, “5.” Then ask them, “What is the uncertainty in 5?” No rational response exists to your question, of course. Likewise no agreed-upon response exists to the question, “What is the S/N value for a single image?” Nonetheless, many programs, including PixInsight (see here), attempt to numerically circumvent the problem, probably with varying degrees of success. As of this writing (May, 2020), Juan Conejero posed a comment on the PI forum to the effect that the current noise evaluation is going to be replaced by a better one in an upcoming release. Noise evaluation is far from cut-and-dried.
Now, whatever your personal take-away from the above might be, we move on to discuss alternative variables for assessing subframe qualities or weights. Other clearly measurable variables do exist in an image, and speak to elements of the relative quality of an image compared to the ensemble of subframes. Thus they may well be more adjusted to the particular type of target you have.
Relevant Quality Variables
Other image parameters, besides the frail S/N ratio, speak to a subframe’s worth in a stack of similar subframes. Often those variables receive scrutiny during frame-by-frame blink comparison. For instance, visually assessing star ellipticity, FWHM, and other measures (e.g., using blinking) could help an image processor to eliminate wildly deviant frames. But one might argue that a frame with some modest degree of star ellipticity, for instance, might suffer a justifiably lower weight without being completely eliminated.
Besides the obviously inferior frames, we might wonder if some variable used to quantify image quality might sometimes be misleading. For instance, does FWHM or ellipticity decrease as a light haze or sky glow impinges on the imaged scene? I’m not sure about the answer, but it worries me that it might. Sometimes the number of stars in an image strongly, negatively correlates with FWHM and even ellipticity! Maybe those variables should not have a large say in a final frame’s weight? I tend to favor StarSupport as an important subframe-weight parameter. If the sky becomes hazy or light pollution rises, StarSupport decreases, as it would if the focus drifted, turbulence increased or tracking-accuracy declined. All these either spread the star light more broadly so that fainter stars fail to be recognized or mask the fainter stars with an increase in the background. However, Mike Schuster (here) notes that under-sampled images (wide field, low resolution images), may not separate stars and noise well. Also, subs with abundant shot noise may give false, elevated star counts. This can be somewhat ameliorated during calibration and using CosmeticCorrection.
SWT also includes two variables that encode the behavior of the median value of a subframe: MedianHi” and “MedianLow”. The former could be used if you believe that higher values of the median indicate better subframes, as might be the case if a nebula pervades the image. The former could be used if you believe that smaller values of the median indicate better images, such as an image of a small galaxy in a field of stars and darkness. Be watchful of these measures, however. You could have a very dark background because you forgot to remove the cover from the camera lens (or…).
Something about SWT’s internal workings
The Less Arbitrary Part—Scaling Within a Variable
Consider a single quality-evaluation variable measured across a number of subframes. That variable will have a range of values from least favorable (XA) to most favorable (XZ). A measured intermediate value of Xi for some subframe image in this set might reasonably be assigned a weight (wi) proportional to its position in the range of values; e.g.,
wi µ (Xi - XA) / (XZ – XA) . Eqn 1
Such a linear relationship could be specified for each variable, i, producing a set of variable-by-variable weights for each subframe. This is the approach used in my SWT with the addition of a “pedestal.”
The More Arbitrary Part—Scaling Among Variables
Combining individual variable weights from Eqn 1 into an ensemble weight involves “user’s prerogatives.” That is, based on your individual experiences and perspectives, and considering the particular attributes of the image-set at hand, the ensemble of within-variable weights can be combined by relative weighting factors (denoted by F). For example, say you measured the variables V1, V2, V3 on some image j. Those variables would, by Eqn 1, have corresponding weights w1,w2,w3 for that one image. Consistent with our individual knowledge and preferences, we would assign weighting factors F1 F2 F3 to each w such that F1 + F2 + F3 = 1. We can then obtain an overall weight, Wj, for our single subframe frame. For example, the kth frame’s weight would be
Wk = F1w1k + F2w2k + F3w3k . Eqn 2
In SWT, the final values of the frame weights also can be rescaled between a pedestal value (minimum frame weight) and 1.0, and nonlinearly gamma-stretched to span that interval, at the discretion of the user.
The Flow of Action
Load images for weighting into SubframeSelector script of PixInsight. Usually the images analyzed in a single pass would be a homogeneous set (for instance, all light frames of a single subject shot through a single filter). Additionally, these should be raw, calibrated and cosmetically corrected frames and not stretched.
Use SubframeSelector’s “Measure” feature to produce a table of values of variables for each frame.
Output the table in a csv format using SubframeSelector’s “Save CSV” button.
Open the SWT workbook and Enable Content, if necessary (top yellow banner).
Select the four variables you want to start, you can select others any time.
Click the Read CSV File button in the Excel spreadsheet. Select and load the desired file.
Adjust weights, Pedestal, Stretch, etc. until you have a satisfactory relationship for accepting and rejecting subframes.
If you change variables in table I, the spreadsheet will re-read the data to implement the new selection.
Click Copy SS Equation button to copy the equation generated by the Subframe Weighting Tool to the clipboard. Then paste the equation into Expressions>Weighting field of the SubframeSelector. Click the arrow at the right of the Expression Weighting field to implement the equation you just pasted.
Set SubframeSelector’s Approval level to the desired value—usually the one you settled upon in SWT. Click the arrow to the right of the field where you pasted the level to implement the new criterion. (Note, your equation in this field should look something like this: “Weight>=0.4”.)
CHECK THAT THE WEIGHTS CALCULATED IN SUBFRAMESELECTOR MATCH THOSE IN SWT. If they do not, either the wrong information was pasted into SubframeSelector or you did not click the arrows to update SubframeSelector to the information you pasted in.
Set SubframeSelector’s name for the new weights it will generate and the output path and click “Output Subframes”. The name SSWEIGHT seems appropriate.
The images output in the previous step may be used in PixInsight’s ImageIntegration procedure, specifying the name you specified for the new weighting variable (e.g., SSWEIGHT). The integrated image now will reflect the user-defined weights.
If you need duplicate sheets for different filters, use the Copy Sheet button.
Another used for the weights generated by SWT is to select a subframe for the reference alignment frame. The subframe with a large number of stars and a small number value for the FWHM would present a logical choice. If the compulsion drives you, you could combine all the fames from every filter on one spreadsheet and select a winner. Alternatively, look for the best Luminosity frame or the best green-filter frame.
The SWT’s User Interface
Input fields have yellow backgrounds. A detected input error turns the offending cell’s background to red. Computed-values cells in the spreadsheet that have a white background or a deep-blue background (e.g., the “WEIGHT” column), should not be edited. Many of them contain equations; others have text designed for special purposes. The bright green cell is the one that is copied to the clipboard for pasting into the weighting equation in the SubframeSelector script. The less bright green cells simply provide a background highlighting the equation.
The discussion now references the spreadsheet entry fields I through V as labeled on the spreadsheets.
Select 4 variables to participate in the weighting from the drop-down lists. You may assign a zero weight to a variable. The fourth variable, at the bottom of the list, is the variable that will be used as the independent variable in the variable-variable cross plots.
The weights [0.0, 1.0] to assign to each of the first three variables. The weight of the final variable is calculated such that the sum of the weights equals 1.0.
Controls for the pedestal and stretch of the distribution of the subframe weights.
Pedestal: controls the minimum subframe weight that will be assigned. At least one subframe will have that weight and at least one weight will be 1.0.
Gamma Stretch: a stretching exponent (> 0) that affects the distribution of the weights within the interval [Pedestal, 1.0].
Norm: This has two values selected from a drop-down menu. An L1-measure weights the variables by their distance from the worst value for each weighting variable. An L2-measure uses the square of that distance. (Use L2 if in doubt. Usually the two give pretty much the same weights.)
Min. Approval Value: If a subframe’s weight is less than this value, that subframe has red markers on the plots and in the tables. Expectedly, SubframeSelector (if fed proper inputs from SWT) will not retain red-marker subframes in its output.
Locate the part of the sub-frame name to display: E.g., say the location of the last character in the ID lies back N characters from the “.” of the file extension. You would enter N-1 in this field to see the ID. The “Trim From…” has a dropdown menu to facilitate trimming from the beginning or end of the frame ID.
The function of the other (yellow) user-input fields should be rather obvious.
Contemplating and Evaluating the Relations among Input Parameters
Before running Subframe selector, blink your images! Images that appear “unlike the others” are also not statically members of the group and will distort the weights. Remove them before using SWT!!! Remove any that have strongly elliptical stars, star trails, high noise, low signal, etc.
To adjust the relative variable Weightings and the Stretch, Pedestal, and Approval level, garner some insights from three sources:
1. The top graph: Does the overall spread of weights look reasonable and functional? For instance, if all the frames are expected (from blinking, say) to have pretty similar qualities, maybe a higher-value pedestal, to compress all the weights to a small range, may be appropriate.
2. The other three graphs: Are the rejected subframes (red) and the best subframe (green) credible given what you know about the image acquisition? Cross-check rejected subframes among graphs and the tabulated data—does rejection/Approval make sense?
3. If need be, examine the frames that have unexpected weights. (Click the “Hyperlink>View” to open the frame in your default viewer, probably PI.)
4. Most importantly, scroll down to examine the correlation table below the graphs: Are some variables strongly correlated? If so, then perhaps you want to down-weight one of the two correlated variables as the other variable partially accounts for its variations already. Also, do the correlations suggest some prevailing effect, such as more stars correlate positively with greater eccentricity…what is that trying to tell you?
5. The “range variability” of each variable (the row above the pasted data): Variables with noticeably smaller ranges than the other variables may indicate that the variations are unimportant (i.e., largely random variations or measurement uncertainties). In that case, down-weighting the narrowly varying variables could be justified. You might look for another variable to use instead: one that varies more widely yet quantifies frame quality as well.
We hope you find this spreadsheet useful. You may contact us through alex@awkml.com . Please report any bugs and suggestions for improvements and additions. Also, in published images, e.g., on Astrobin or Flicker, Simply reference “SWT”- Thanks!
