Hi all,
Today we have released a new tool: DynamicPSF. This long-awaited tool fills an important gap in the set of image analysis tools of PixInsight that we have been suffering during years.
While we write documentation
[1], let me make a brief description and an overall introduction to the features and practical usage of this essential tool.
As its name suggests, DynamicPSF is a dynamic PixInsight tool for PSF (Point Spread Function) modelling. In a nutshell: you click on an image and DynamicPSF looks for a star (or a star-like object) around the coordinates you have clicked at. If something like a star can be found close to those coordinates, DynamicPSF tries to fit a three-dimensional function from a set of sampled image pixels. It then provides a number of useful parameters that describe the PSF in terms of the function fitted.
The practical usage of DynamicPSF is quite similar to that of DynamicAlignment. In fact, I have reused a number of routines and algorithms from DA to write DynamicPSF, although I have reformulated and improved all of them significantly (among other things, this means that you can expect a new version of DA after Summer, including an interactive mosaic building feature and improved accuracy).
This initial version of DynamicPSF can fit elliptical Gaussian and Moffat
[2] functions. An elliptical Gaussian PSF fitting function is defined as:
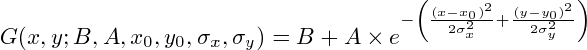
where the parameters are:
B - Average local background.
A - Amplitude, which is the maximum value of the fitted PSF, and also the function's value at the centroid coordinates.
x0,y0 - Centroid coordinates. This is the position of the center of symmetry of the fitted PSF.
sigmax, sigmay - Standard deviation of the Gaussian distribution on the horizontal and vertical axes, measured in pixels.
An elliptical Moffat function is given by:
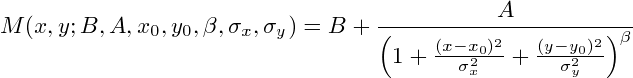
where the parameters are as above and the
beta exponent controls the overall shape of the fitting function. When beta = 1, the above equation corresponds to a
Lorentzian distribution.
In all cases the functions are fitted to ensure that sigma
x >= sigma
y.
DynamicPSF also supports rotated functions. When the difference between sigma
x and sigma
y is larger than or equal to 0.01 pixel (which is the nominal fitting resolution), DynamicPSF fits an additional
theta parameter, which is the rotation angle of the X axis with respect to the centroid coordinates, in the range [0,180[ degrees. For a rotated PSF fit, the x and y coordinates in the equations above must be replaced by their rotated counterparts x' and y', respectively:
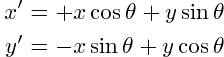
Rotation angles are measured in counter-clockwise direction.
For those users more technically inclined, DynamicPSF implements the
Levenberg-Marquadt algorithm as a
model trust region minimization procedure (the algorithm minimizes the mean absolute deviation of the fitted function from the sampled data). The underlying implementation is a custom adaptation of the
CMINPACK library to the PixInsight/PCL framework.
For all fitted PSFs DynamicAlignment computes a set of additional parameters:
FWHMx - The full width at half maximum on the X axis. FWHM is a well-known, simple and easy to understand measurement of the size of a star as seen on the image.
FWHMy - The full width at half maximum on the Y axis. For circular functions, we have FWHMy = FWHMx.
MAD - The mean absolute deviation of the function fitted with respect to the actual sampled pixel values. This parameter is a robust estimate of the
goodness of fit, or in other words, it tells you how well a star can be represented by the fitted function. Higher MAD values denote comparatively poorer fitting quality.
DynamicPSF can also search for the function that best represents the sampled image data in terms of minimizing MAD. Finally, instead of fitting elliptical PSFs you can tell DynamicPSF to fit circular functions, where sigma
x = sigma
y and theta = 0. For raw images with high noise levels and/or strongly undersampled images circular functions can usually be more robust and hence preferable (robustness is an extremely desirable property in the PSF modelling problem). The uncertainty introduced by additional parameters (two axes and a rotation angle) can lead to meaningless results for these images.
Now the obvious question is: what is DynamicPSF useful for? This question has many and interesting answers. Modelling the PSF of an image or a set of images allows us to make quantitative assertions on important acquisition and instrumental conditions, such as seeing, tracking quality, focus quality, optics performance and focal plane geometry, among others.
There are much more details and practical usage considerations than this introduction, which we'll try to cover in the documentation. I just hope these notes will help you start using this new tool, which is the result of an intense development work we've been undertaking for several months. Please feel free to ask anything related to this tool in this thread and we'll try to do our best to solve your doubts. As is customary in all PixInsight implementations, DynamicPSF is the high-precision and highly versatile image analysis tool that our users need and deserve.
Enjoy!
__________________
[1] You can rest assured that we'll write documentation for this tool. These release notes will be reused to write the documentation, so this text is not a waste. So it is really not necessary that you insist in this regard :)[2] Moffat, A. F. J., A Theoretical Investigation of Focal Stellar Images in the Photographic Emulsion and Application to Photographic Photometry, Astronomy and Astrophysics, Vol. 3, p. 455 (1969)