Arbitrary Distortion Correction with StarAlignment
Tutorial by Juan Conejero (PTeam)
This document is an adaptation of several tutorials posted by the author on PixInsight Forum in July and December of 2013.
Introduction
StarAlignment is a sophisticated tool for automatic image registration of deep-sky images using detected stars as alignment references. Versions published before mid-2013 had several limitations that we have addressed in the recent versions of this essential tool. One of the most important problems was the lack of a robust and consistent support for arbitrary distortions. This was a severe limitation for registration of dithered wide-field images and images acquired with different optical systems, as well as for construction of wide-field mosaics.
In this document I'll describe the improvements and new features that we have implemented in recent versions of StarAlignment, along with some practical usage recommendations.
New Star Detector
Many of the most important problems in previous versions of StarAlignment were related to its star detection routine. Star detection is not a trivial task by any means. On one hand, a star detection routine has to be exhaustive: in general, we want to detect as many stars as possible. On the other hand, there are additional requirements that complicate the design and implementation of a good star detection algorithm: it must be scale-invariant (given two images of the same subject at different scales, we want to detect two compatible sets of stars); it must be robust to illumination changes (we need to detect stars on free sky regions and on extended nebular regions); it must be robust to multiple stars and crowded fields, and it must be able to distinguish between true stars and small nonstellar structures such as bright nebular features, hot pixels, and cosmic rays. In addition, it should be highly controllable (for example, we need control over detection sensitivity and rejection of elongated stars), computationally efficient, and accurate.

Example of star detection.
A – Too complex structure; star parameters uncertain.
B – Crowded, but an accurate position is feasible.
C – Crowded, cannot compute an accurate position.
D – Too dim star (as per current detection sensitivity).
The old star detection routine was based on a multiscale algorithm. This wavelet-based algorithm is very robust to illumination variations and is also very controllable and efficient, but it has a serious drawback: its multiscale nature makes it strongly scale-dependent. For example, the set of detected stars on a relatively small crop of an image were different from the stars detected on the whole image for the same region. In general, star detection on images subject to relatively small scale variations led to incompatible sets. This was an important limiting factor for the applicability of the StarAlignment tool.
Most of these limitations are now overcome by the new star detection algorithm. The new algorithm is robust to strong scale variations, considerably faster than the old algorithm, and more accurate. It is somewhat less controllable, but this doesn't cause practical problems in most cases. For practical use of the StarAlignment tool, you can just ignore the star detection section in virtually all cases, as happened in previous versions. It will just work faster and better.
A JavaScript implementation of the new star detection algorithm is the StarDetector core object, which is part of the PixInsight JavaScript Runtime, and hence is available in all PixInsight distributions.
New Star Matching Descriptors
Previous versions of the StarAlignment tool used triangle similarity[1][2] to find star pair matches between images. Triangle similarity is invariant to some affine transformations: translation, rotation, and uniform scale variation. Clearly, this excludes any form of local distortion, and also excludes more general linear transformations such as projective transformations (homographies). As a result, previous versions of StarAlignment were using a too rigid star matching device, and despite some strategies that I had implemented to palliate this problem (such as favoring generation of small-scale triangles to improve tolerance to large-scale deformations), triangle similarity was limiting the applicability of this tool considerably.
The new version of StarAlignment uses a different geometrical device to find star pair matches: polygonal descriptors.[3][4] Quadrilaterals (AKA quads), pentagons, hexagons, heptagons and octagons are supported in the current StarAlignment version. By default, pentagons are used. A pentagon descriptor looks like the following figure.
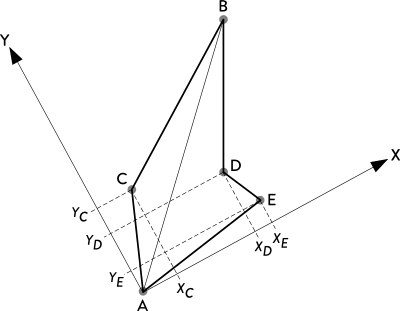
Without entering many details, the two most distant stars of a polygon are used to define a local coordinate system, where the other N–2 stars (N being the number of stars, equal to the number of polygon sides) are identified by their local coordinates to form a hash code of length 2×(N – 2). With the pentagon descriptor shown above, the local coordinate system would be defined by the pair {A,B}, and the descriptor hash code would be the sequence {XCYCXDYDXEYE} of local coordinates in lexicographical order. Polygonal descriptors are invariant to affine transformations (translation, rotation and scaling), and if properly implemented, they are also quite robust to global projective transformations and local distortions.
Besides invariance and robustness to geometrical transformations, the strength of polygonal descriptors lies in their low uncertainty. A polygon formed with N stars associates N–2 triangles. For example, a quad descriptor is equivalent to two triangles tied together. Hence, in the context of searching for a descriptor among all of the stars in an image (as part of a star matching routine), the uncertainty of a quad is half the uncertainty of a single triangle, the uncertainty of a pentagon is one third, and so on. Less uncertainty leads to less false star pair matches, so the initial set of putative star pair matches contains a smaller proportion of outliers, and the overall image registration process is considerably more robust and efficient even under difficult conditions.
Arbitrary Distortion Correction
For the local distortion correction routine I have designed and implemented a successive approximations scheme. The whole algorithm is rather complex, but it basically works as follows. The first iteration generates an initial, purely linear (projective) registration model with the initial set of detected stars. At each subsequent iteration, the current registration model is applied using thin plates to all detected stars, and a new set of putative star pair matches is generated. To this set a RANSAC (RANdom SAmple Consensus) routine[6] is applied successively with increasing tolerances, trying to find a new model able to match more stars than the preceding one. Each iteration step of this algorithm works as a predictor-corrector step: the current model predicts a set of putative star pair matches, which RANSAC validates and corrects to fit a homographic projection. The concept is similar to predictor-corrector numerical integration algorithms widely used for solar system ephemeris calculation.
At each iteration, the new registration model is more flexible and tends to match more star pairs. The algorithm converges to a solution where the model predicts star positions than can no longer be corrected to match the reference image. An ideal registration model would predict star positions that match perfectly their reference image counterparts. If this happens, the RANSAC correction to the set of predicted star positions is the unit matrix:
1 0 0
0 1 0
0 0 1
So we stop the local distortion correction algorithm when we achieve a correction model very similar to the unit matrix. The iteration stop criterion is:
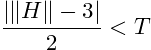
where H is the corrector transformation matrix, T > 0 is the distortion residual parameter, and ||·|| is the matrix modulus operator (the sum of the absolute values of all matrix elements).
Distortion Example I: Nonuniform Scaling
Let's put a few examples to demonstrate the improved performance of the new StarAlignment version. I'll start with a moderately nontrivial problem: nonuniform scaling.
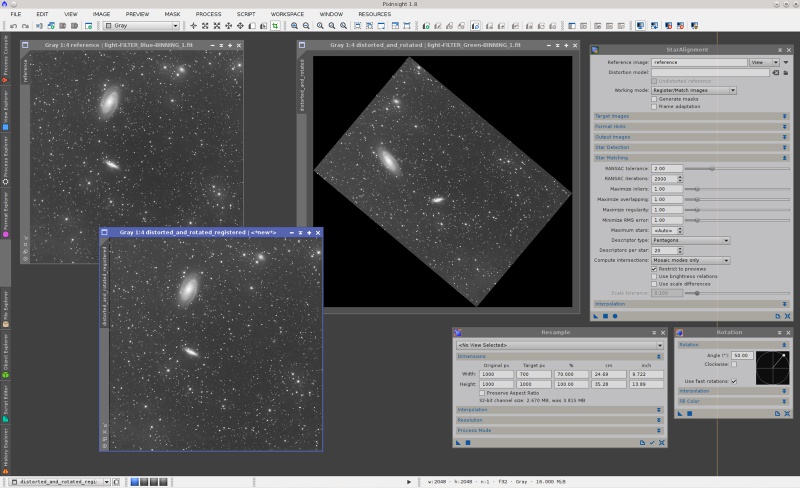
On the screenshot above, we have two master light frames acquired with blue and green filters, respectively. It is important to point out that they are two different images, not a duplicated image. The images are linear and have automatic screen stretch functions applied. The green frame, namely the "distorted_and_rotated" view, has been transformed as follows:
- Resample: horizontal scaling factor = 70%, vertical scaling factor = 100% (preserve aspect ratio disabled).
- Rotation: 50 degrees counter-clockwise.
StarAlignment has registered these images perfectly with default parameters. This was very difficult or impossible with the old StarAlignment tool.
Let's make things slightly more difficult: two consecutive distortion-rotation steps to turn the image into a trapezoid:
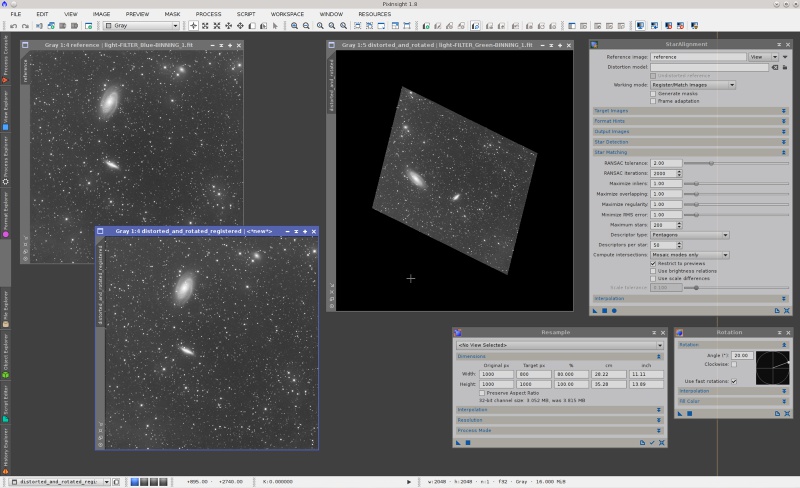
This time the sequence of operations is:
- Resample: horizontal scaling factor = 80%, vertical scaling factor = 100% (preserve aspect ratio disabled).
- Rotation: 50 degrees counter-clockwise.
- Resample: horizontal scaling factor = 80%, vertical scaling factor = 100% (preserve aspect ratio disabled).
- Rotation: 20 degrees counter-clockwise.
In this case I have just increased the number of descriptors per star from its default value of 20 to 50. Then the image has been registered without problems.
Note that the above examples are extreme cases: By default, StarAlignment has not been designed to solve this kind of problems. Yet it can deal with them easily using default or nearly default parameters, thanks to a complete rewrite of the whole star matching routine.
But we can now do much better than this with the new local distortion correction feature.
Distortion Example II: Central Dilations
Complex affine transformations that were problematic or even impossible with previous versions of StarAlignment are now handled without any problems. The following script applies a warp transformation to the active image:
function affineWarp( image, warpFactor )
{
var c = image.bounds.center;
var r = c.distanceTo( 0, 0 );
var w = image.width;
var h = image.height;
var work = new Image( image );
for ( var y = 0; y < h; ++y )
for ( var x = 0; x < w; ++x )
{
var dx = x - c.x;
var dy = y - c.y;
var dr = Math.sqrt( dx*dx + dy*dy );
var fr = warpFactor*dr/r;
var fa = Math.atan2( dy, dx );
var fx = fr*Math.cos( fa );
var fy = fr*Math.sin( fa );
image.setSample( work.interpolate( x-fx, y-fy ), x, y );
}
}
var window = ImageWindow.activeWindow;
var view = window.mainView;
view.beginProcess();
affineWarp( view.image, 300 );
view.endProcess();
Our warp factors are expressed in pixels. Since this script only transforms the first channel of the active image, its effect is clear when we apply it to a color image (with a warp factor of 150 pixels for better visualization):

For positive warp factors, this transformation is a linearly increasing radial upscaling applied from the center of the image, where the scaling factor is equal to one, to the corners, where the deformation is equal to the warp factor. If you don't believe that this is an affine transformation, look at the following images (original and warped):


The transformation is affine because it preserves parallelism of straight lines. Technically this is known as central dilation. The new version of PixInsight can register images transformed this way without problems, and of course it can register them with both triangle similarity and polygonal descriptors.
Distortion Example III: Optical Distortions
So far this may not seem very impressive, since central dilations are just affine transformations, after all. So let's try with nonlinear distortions to really put the tool into test. The following script performs a simulation of second order and fourth order optical distortions, also known as barrel, pincushion, mustache, etc.
function distortion( image, K1, K2 )
{
if ( typeof( K1 ) == "undefined" )
K1 = 0;
if ( typeof( K2 ) == "undefined" )
K2 = 0;
var c = image.bounds.center;
var w = image.width;
var h = image.height;
var work = new Image( image );
for ( var y = 0; y < h; ++y )
for ( var x = 0; x < w; ++x )
{
var dx = x - c.x;
var dy = y - c.y;
var r = Math.sqrt( dx*dx + dy*dy );
var r2 = r*r;
var k = K1*r2 + K2*r2*r2;
var xu = x + dx*k;
var yu = y + dy*k;
image.setSample( work.bounds.includes( xu, yu ) ?
work.interpolate( xu, yu ) : 0, x, y );
}
}
var window = ImageWindow.activeWindow;
var view = window.mainView;
// Barrel distortion
view.beginProcess();
distortion( view.image, 5.0e-08 );
view.endProcess();
This script implements (partially) Brown's classical distortion model.[5] The K1 and K2 function arguments are the second and fourth order distortion factors, respectively. If we apply the above script to the same M81/M82 image as before, we cause a rather strong barrel distortion. The new version of StarAlignment can register the distorted image easily, thanks to its new arbitrary distortion model feature. You can see the applied parameters on the following screenshot.
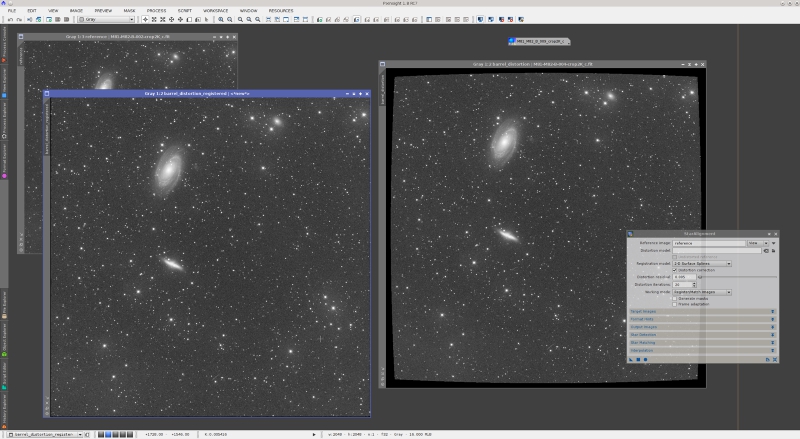
All parameters are by default except distortion correction, which has been enabled, and registration model, which has been set to "2-D surface splines". A surface spline, also known as thin plate, is an extremely flexible interpolation device that can be used to model nonlinear transformations. Thin plates are also necessary to correct for differential distortion, which is the kind of deformations that must be corrected to build accurate wide-field mosaics.
To evaluate the accuracy of StarAlignment with distortion correction, here is an animation of a small crop on the bottom left corner of the image, enlarged 3:1:

Let's put a more difficult example: fourth order distortions. If we change the parameters of the distortion function in the above script to K1=1×10–7 and K2=–5×10–14, we get the following mix of pincushion and mustache distortion:
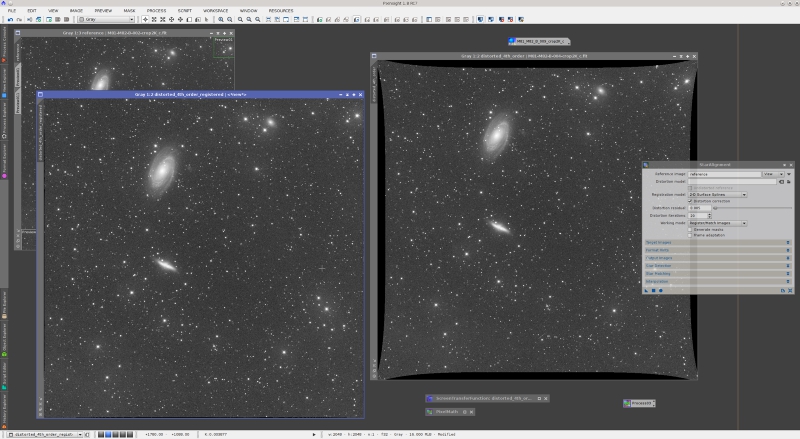
Again, StarAlignment can deal with this complex distortion:

Of course, the new distortion correction feature has some limitations. On the animation above, note that the stars at the very corners of the registered image are still displaced with respect to the reference image. Other than these four small regions, subpixel registration accuracy is constant for the whole image. A better result could be achieved quite easily by tweaking some star matching parameters, but I have preferred to show the result with default parameters.
The new distortion correction capabilities of StarAlignment allow for accurate registration of images from different telescopes, something that was problematic with previous versions. In many cases, accurate registration of dissimilar images is achievable even without enabling the distortion correction feature, thanks to the flexibility of polygonal descriptors.
Improved Mosaic Construction
Mosaic construction also benefits greatly from distortion correction. The following screenshot shows an absolutely wonderful mosaic by Thomas W. Earle, which you can see finished on a gallery forum post.
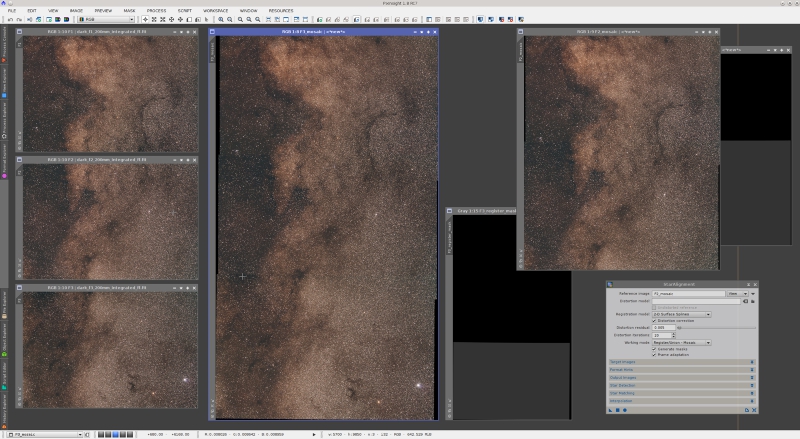
This is a three-panel mosaic of the Milky Way in Aquila, acquired with a Canon EF 200 mm f/2 lens, stopped down to f/4. Wide-field mosaics are difficult due to differential distortions. Basically, the problem is that we are mixing images on areas where they are distorted differently, often with opposite sign curvatures. Previous versions of the StarAlignment tool did a good job thanks to the application of thin plates and small-scale triangle generation, but there was considerable room for improvement. The current version provides a significant improvement.
The following crops are the result of subtracting the registered second (middle) mosaic panel from the reference first (top) panel. The differences in the residuals clearly show the accuracy and correctness of the image registration task.

Registration residuals, projective registration model, no local distortion correction.

Registration residuals, thin plates registration model, no local distortion correction.

Registration residuals, thin plates registration model with local distortion correction.
The visible residuals after registration with local distortion correction (third image in the above list) are due to differences in lateral chromatic aberration between mosaic frames, not to registration errors. The following animation shows the same registration residuals on a crop of the mosaic seam area at the original resolution of the image.

We know that the residuals after local distortion correction are due to lateral chromatic aberration because each residual consists of two lobes, one red and the other green-bluish. Between these lobes there is the star's brightness peak, which has been removed after subtracting the registered images, denoting an accurate registration. After registration without local distortion correction, the residuals clearly show alignment errors.
Distortion Models
In addition to the local distortion correction feature, the new version of StarAlignment supports externally defined distortion models. A distortion model can be used to pre-correct the images for optical aberrations such as field curvature, lateral chromatic aberration and other arbitrary geometrical transformations. This way the image registration process can work with undistorted alignment references.
StarAlignment distortion models must be plain text files in standard CSV (Comma-Separated Value) format. Formally, a valid distortion model can be described as:
<distortion-model>:
<model-header>
<model-nodes>
<model-header>:
<model-device>, <model-order>opt
<model-device>: one of:
2DSurfaceSpline
ThinPlate
<model-order>: one of:
2
3
4
5
<model-nodes>:
<minimal-node-set>
<extended-node-set>opt
<minimal-node-set>:
<model-node>
<model-node>
<model-node>
<extended-node-set>:
<model-node>
<extended-node-set>opt
<model-node>:
<x>, <y>, <dx>, <dy>
where <x>,<y> are the image coordinates of the point of application of a distortion vector, and <dx>,<dy> define the vector's magnitude and direction. The four node elements are floating point numbers expressed in pixels. As exposed by the above formal definition, a valid distortion model has three or more nodes.
In this initial release only thin plate distortion models are supported, so 2DSurfaceSpline and ThinPlate are synonyms. The model order parameter refers to the derivative order of continuity. Second-order models are usually more than sufficient to represent even wildly nonlinear transformations, so they are recommended by default. Third-order models can represent very strong small-scale distortions. Higher order models can easily become unstable and are thus discouraged for normal use.
Let's put an example where a distortion model is necessary for successful image registration. The following script applies a cylinder deformation:
function cylinder( image, warpFactor )
{
var f = new File;
f.createForWriting( "/tmp/dmodel.csv" );
f.outTextLn( "ThinPlate,2" );
var w = image.width;
var h = image.height;
var r = 0.5*h;
var work = new Image( image );
for ( var y = 0; y < h; ++y )
for ( var x = 0; x < w; ++x )
{
var fy = warpFactor*(y - r)/r;
var yd = y - fy;
image.setSample( (yd >= 0 && yd < h) ?
work.interpolate( x, yd ) : 0, x, y );
if ( y % 100 == 0 )
if ( x % 100 == 0 )
f.outTextLn( format( "%10.4f,%10.4f,%10.4f,%10.4f", x, yd, 0, fy ) );
}
f.close();
}
var window = ImageWindow.activeWindow;
var view = window.mainView;
view.beginProcess();
cylinder( view.image, -500 );
view.endProcess();
The script applies the geometrical transformation and generates the corresponding distortion model in CSV format, suitable to be used with StarAlignment.
When a strong deformation factor is applied, the cylinder transformation poses a very difficult problem for image registration. The next screenshot is an example.
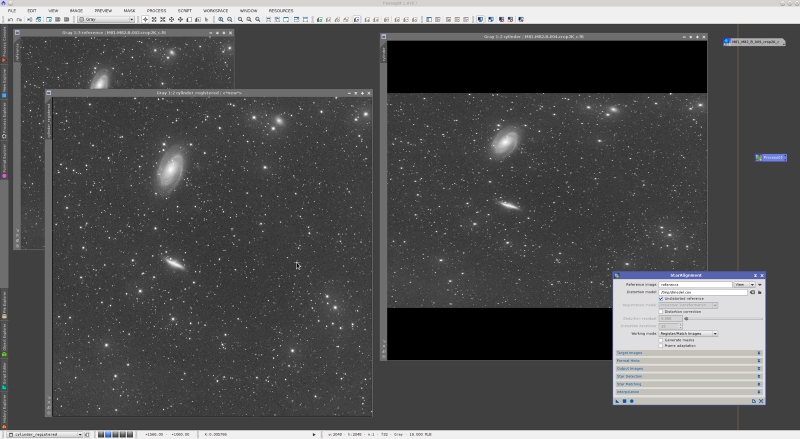
In this case, the undistorted model parameter has been enabled because the registration reference image has no distortion. With the help of a model, StarAlignment registers this image immediately. However, without a distortion model, the image shown in the screenshot above cannot be registered, even with local distortion corrections.
Higher Accuracy and Robustness: Approximating Surface Splines
As I have said in the preceding paragraphs, StarAlignmen't distortion correction algorithm uses two-dimensional surface splines, also known as thin plates, as a non-rigid mathematical model to describe the geometrical transformation necessary to register two images. Surface splines are extremely adaptable to local function variations, which makes them particularly appealing as flexible interpolating devices in many image analysis and processing tasks. We already have been using them for a long time in tools such as DynamicBackgroundExtraction and DynamicAlignment.
In versions released before November of 2013, StarAlignment's distortion correction has been using interpolating surface splines. In an interpolating spline, each data point is reproduced exactly by evaluation of the spline functions. In the case of image registration, this means that for each matched star pair, the target image star is registered exactly on its reference image counterpart. This sounds good at first sight, since after all, "perfect" star matches guarantee a "perfect" image registration. But as you surely know if you've been involved in this image processing business for some time, the words "perfect" and "exactly" almost invariably denote a questionable procedure or implementation.
As implemented in our StarAlignment tool, distortion correction by interpolating surface splines works very well most times. However, it can work not so well sometimes, and I'm going to put a "good" example of this problem here. Before you continue reading and getting scared by some image comparisons, the good news is that (1) these problems are now fixed with the new implementation, and (2) these problems only happen in particularly unfavorable cases.
The following screenshot shows PixInsight 1.8.0 Ripley while working on a two-frame mosaic by Vicent Peris, who has released the final image on PixInsight Forum's gallery. The mosaic covers a nice region of the Large Magellanic Cloud close to the Tarantula nebula.
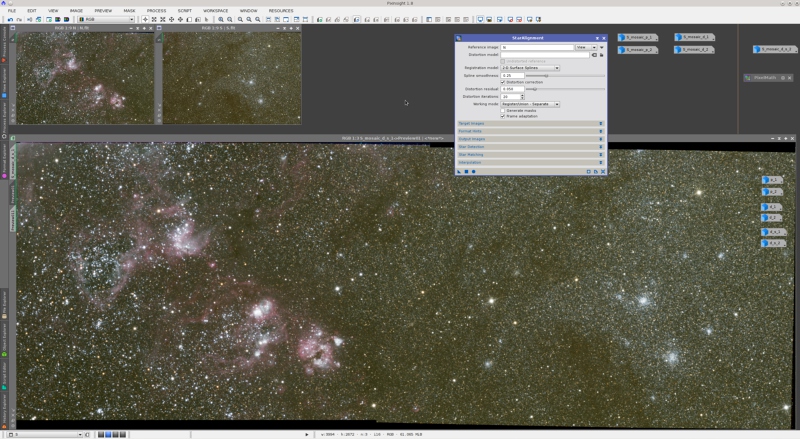
Although not evident at first sight, this data set has two properties that expose the weakness of interpolating splines used as image registration models:
- It is a wide-field image crowded of stars.
- Seeing was not particularly good, so the stars have quite flat profiles.
The first property increases the probability of overlapped, colliding, or very close star images. Although StarAlignment's star detection routine does a good job trying to avoid such problematic star images as registration references, decreasing the average distance between nearby star images doesn't help to compute accurate star positions. The second property makes things even worse for star detection, since a flat star profile increases the uncertainty in the computed star position. As a result, the registration model is less accurate, more uncertain, and contains a non-negligible amount of mistakes. If we use interpolating surface splines to reproduce all star pair matches exactly, the result is a very good example of the difference between numerical accuracy and model adequacy:

To generate the above animation, we have registered both mosaic frames with StarAlignment working in Register/Union - Separate mode and the new Spline smoothness parameter set to zero. This effectively forces StarAlignment to use pure interpolating splines, which has been the only option available until now. To combine both mosaic frames in a way that maximizes registration differences visually, we have applied the maximum operator with the following PixelMath expression:
max( $T, the_other_mosaic_frame )
on a full preview on one of the mosaic frames. What you are looking at on the above animation is the result of excessive local adaptation, or excessive flexibility in the registration model.
Enter approximating surface splines. In contrast to interpolating splines, approximating splines don't reproduce all data points exactly. Instead, approximating splines introduce some degree of smoothness in the computed registration model. This is a more realistic approach because it assumes that there are errors in the computed star positions, or in other words, that the star positions are really not known exactly, but are just approximations.
To understand how approximation works as opposed to interpolation, consider the following 256x256 pixels grayscale image.

For a moment, forget that this is an image of stars; just take it as a set of scattered measurements of some process represented as varying intensities on a square matrix.
With a simple script in PixInsight, I have generated an interpolating 2-D surface spline from 1024 pixels of the above image, distributed on a regular lattice at intervals of 8 pixels (or a grid of 32x32 interpolation points). When we use this spline to interpolate the original image, we get the following result:
Since the interpolating spline reproduces all data points exactly, we get a wildly varying representation because the original data also vary strongly at small scales. This is an accurate representation of the original data set, but it is not necessarily an accurate representation of the underlying true function.
With approximating surface splines we can get a much better view of the data from a less local, more global perspective. A nice feature of approximating surface splines is that we can control the degree of regularization, or smoothness, with a single numerical parameter:
Now that you know how it works, let's repeat the same mosaic with the new Spline smoothness parameter of StarAlignment set to its default 0.25 value:

Here are animations of the same area zoomed 8:1:


For a better comparison, this is the same region of the mosaic generated using a projective registration model without distortion correction:

The best part of this new feature is that it works very well with its default parameter value in virtually all cases, so you won't have to worry about a new parameter: StarAlignment remains a tool that "just works", and that's even more true with approximating surface splines.
Some Usage Tips
-
Unless it is really necessary, don't use the distortion correction feature. In general, distortion correction is only necessary in two cases:
- Registration of images acquired with different telescopes or lenses.
- Wide-field mosaics.
If the images being registered are not subject to differential distortions, applying distortion correction won't provide more accuracy. It will only slow down the process.
- Distortions caused by dithering of wide-field images can now be fixed with default StarAlignment parameters. Distortion correction is not normally necessary in these cases.
-
Polygonal descriptors cannot work under specular transformations (horizontal or vertical mirror). If you have mirrored images (for example, images acquired with a Newton telescope and a refracting telescope being registered in the same batch), you have two options:
- Either apply the appropriate mirror operation with the FastRotation tool prior to image registration,
- Or use triangle similarity for image registration. On the StarAlignment tool, open the Star Matching section and select "Triangle similarity" as the value of the "Descriptor type" parameter.
-
To verify the correctness of image registration results you can generate residual images. Use the PixelMath tool to subtract the registered and reference images and carefully inspect the result. For example, assuming that you have "reference" and "registered" images, this PixelMath expression:
registered -- reference
computes the absolute value of the difference. Ideally, if both images are accurately co-registered, the difference image should only contain noise and some residuals due essentially to focusing and seeing differences, along with objects that are only present on one of the images, such as cosmic ray impacts and satellite trails. There can also be residuals caused by differential optical aberrations, such as lateral chromatic aberration in wide field mosaics. - For registration of very low-SNR images, you may need to use the noise reduction parameter (Star Detection section). The new star detection routines are faster and more accurate, but they are not well suited to work under heavy noise. The new noise reduction parameter solves this problem.
References
[1] Francisco G. Valdés et al. (1995), FOCAS Automatic Catalog Matching Algorithms, Publications of the Astronomical Society of the Pacific, 107, pp. 1119–1128.
[2] M. Marszalek, P. Rokita (2004), Pattern Matching with Differential Voting and Median Transformation Derivation, Computer Vision and Graphics (Computational Imaging and Vision Series), 32, pp. 1002–1007.
[3] D. Lang, D. W. Hogg, K. Mierle, M. Blanton, and S. Roweis (2010), Astrometry.net: Blind astrometric calibration of arbitrary astronomical images, The Astronomical Journal (AJ), vol. 37, pp. 1782–2800.
[4] G.D. Evangelidis, C. Bauckhage (2011), Efficient and Robust Alignment of Unsynchronized Video Sequences, German Association for Pattern Recognition (DAGM) 2011, Frankfurt.
[5] Brown, D. C. (1966), Decentering Distortion of Lenses, Photogrammetric Engineering, vol. 32, No. 3, pp. 444–462.
[6] Martin A. Fischler, Robert C. Bolles (1981), Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography, Communications of the ACM, Vol. 24 No. 6, pp. 381–395